Omar Shehata
Measuring the size of the world with 2 sticks & a sprinkle of maths
From Omar's notebook.
Below is a pitch for an interactive art exhibit on measuring the radius of the Earth the way the ancient Greeks did — no fancy technology, just observing shadows on sticks, and some math.
It feels so empowering to me that we can measure the vastness of the world with our little minds. Lots of people have written on this (see Khan Academy article).
What makes this piece unique and never been done before is you get to do this yourself:
- The app shows you what time of day to do the measurement
- It asks you to find a friend somewhere else on Earth at a few suggested locations to take the other measurement (or helps connect you with people who want to do this)
- Together, you've measured the size of the world!
I want people to feel empowered. And to feel connected.
I often feel powerless at the scale and magnitude of the world. It feels silly to get out in the street with a stick and measure its shadow. But I think there is a magic in doing this, with others who care. To take what feels like insurmountable task, and actually do it. Together.
How it works
I used a JavaScript mapping library to create the demo videos below. The final app will allow the user to walk through these steps on any location on Earth.
The story of how the Greeks did it starts in the south of Egypt:
This is the northernmost latitude at which the Sun is ever directly overhead at noon. Below I adjust the time of day/year to be noon, around the summer solistice (June). There is no shadow cast when the sun is directly overhead.
We look up to confirm the sun is indeed directly overhead!
Now we do the same thing, at the same time, north of Egypt, in Alexandria. If the Earth was flat, then the stick here would also cast no shadow.
But we do see a shadow! If we do this in real life, that is proof that the Earth is curved.
Measuring the shadow, it is 8.11 meters.

Measuring the stick, it is 60.03 meters.

We also need the distance between the sticks, it's about 850,679.42 meters (the Greeks computed this by walking across the country and counting steps!)
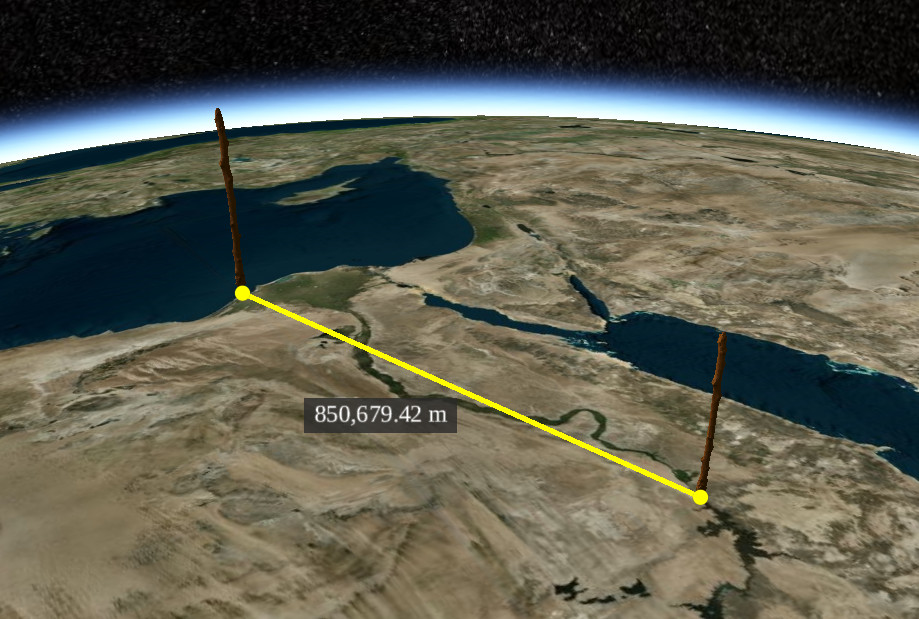
Finally we do some trignometry, assuming the Earth is a perfect circle. Image below from Khan Academy.
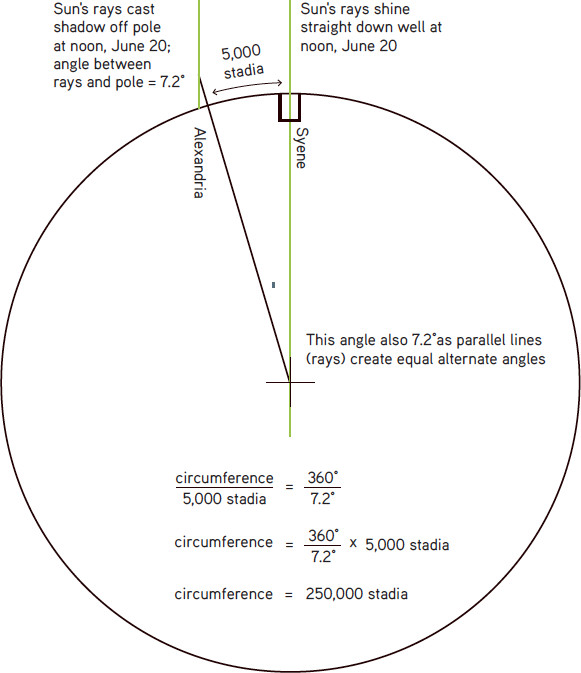
Those numbers give us an answer of 398,317,64.4 meters. That's ~39,800 km. The right answer? 40,000 km. So we're only about 0.6% off!
And that's how you compute the size of the world using 2 sticks, their shadows, and your mind!
Implementation notes
- I think measurements can be taken at any time of the year, at any two locations on Earth that are sufficiently far apart. The software should help the user with this.
- The software can also take into account different sizes of sticks used to take the measurement.
- It would be really cool if this is exhibited at two specific museum locations on Earth where they can make those measurements on site with people and get their answers, and share the pictures of them with the sticks.
- Would be nice to find a way to measure the shadow from a picture, given the stick length. To make it easier for others to validate each other's work.